基于相关滤波器(Correlation Filters)的 MOSSE 算法
Contents
本文将会从 相关滤波器 的相关理论进行展开,讲述如何将信号处理领域的 相关滤波器 融入到目前比较热门的 目标追踪 领域,以及对 MOSSE 算法进行了介绍。
若有错误,还请批评指出。
相关滤波器
没错,这个滤波器的名字就叫做 相关滤波器(Correlation filters),也叫 判别相关滤波器(Discriminative correlation filters,DCF)。它是将信号处理领域中的 信号相关性理论 引入到 目标追踪 领域中的一种方法。
具体思想是:通过使用信号的相关性来描述两个因素之间的联系,将 目标区域 与 待检测的区域 比作信号,并计算这两个区域之间的相关性,相关性越大,则滤波器得到的响应也就越大,最后得到相关性最大的区域就是目标区域,即跟踪区域。
实现步骤可分为如下三步:
- 首先,对已经跟踪出的多个目标区域进行特征提取,通过训练这些特征得到一个滤波器模板;
- 然后,用训练好的滤波器与下一帧中的待检测的区域进行相关性的计算,将相关性最大的区域(最大响应点所在的区域)设置为下一帧中目标预测的位置;
- 最后,提取以目标位置为中心的特征,用新位置区域再次训练并更新相关滤波器,通过不断循环以上步骤进行预测,可达到实时跟踪的效果。
这里有一个 相关性 的概念,可分为如下两种:
- 互相关(cross-correlation),在信号处理领域中,互相关是用来表示 两个信号之间相似性的一个度量,通过与已知信号的比较,以此用于寻找未知信号中的特性。
- 自相关(auto-correlation),也叫序列相关,是一个信号于其自身在不同时间点(频域)的互相关,也就是两次观察之间的相似度对它们之间的时间差的函数。
对于 $ f $ 和 $ g $ 这两个信号量,它们之间的相关性如下所示:
$$ (f \star g)(\tau) = \int_ {\infty} ^ {-\infty}{f ^ *}(t)g(t + {\tau})dt \qquad(1) $$
$$ (f \star g)(n) = \sum_{-\infty} ^ {\infty} {f ^ *} [m]g(m + n) \qquad(2) $$
互相关 实质上类似于两个函数的卷积。
式中,$ f ^ * $ 表示 $ f $ 的共轭复数,这种相关性表示的就是两个函数在某个时刻 $ \tau $ 的相似程度。由于存在时间差,所以要想得到最大值,就需要将其中一个变量进行平移。而 $ g(t + {\tau}) $ 就表示将 $ g $ 平移 $ {\tau} $ 个时刻。
相关滤波 在 目标跟踪 方面主要是通过设计一个滤波器模板,使得当该模板作用在目标上时,得到最大的响应。
目前针对视频的目标追踪方法有三大方向:深度学习方向、相关滤波方向 以及 其它传统方法。如下图所示:
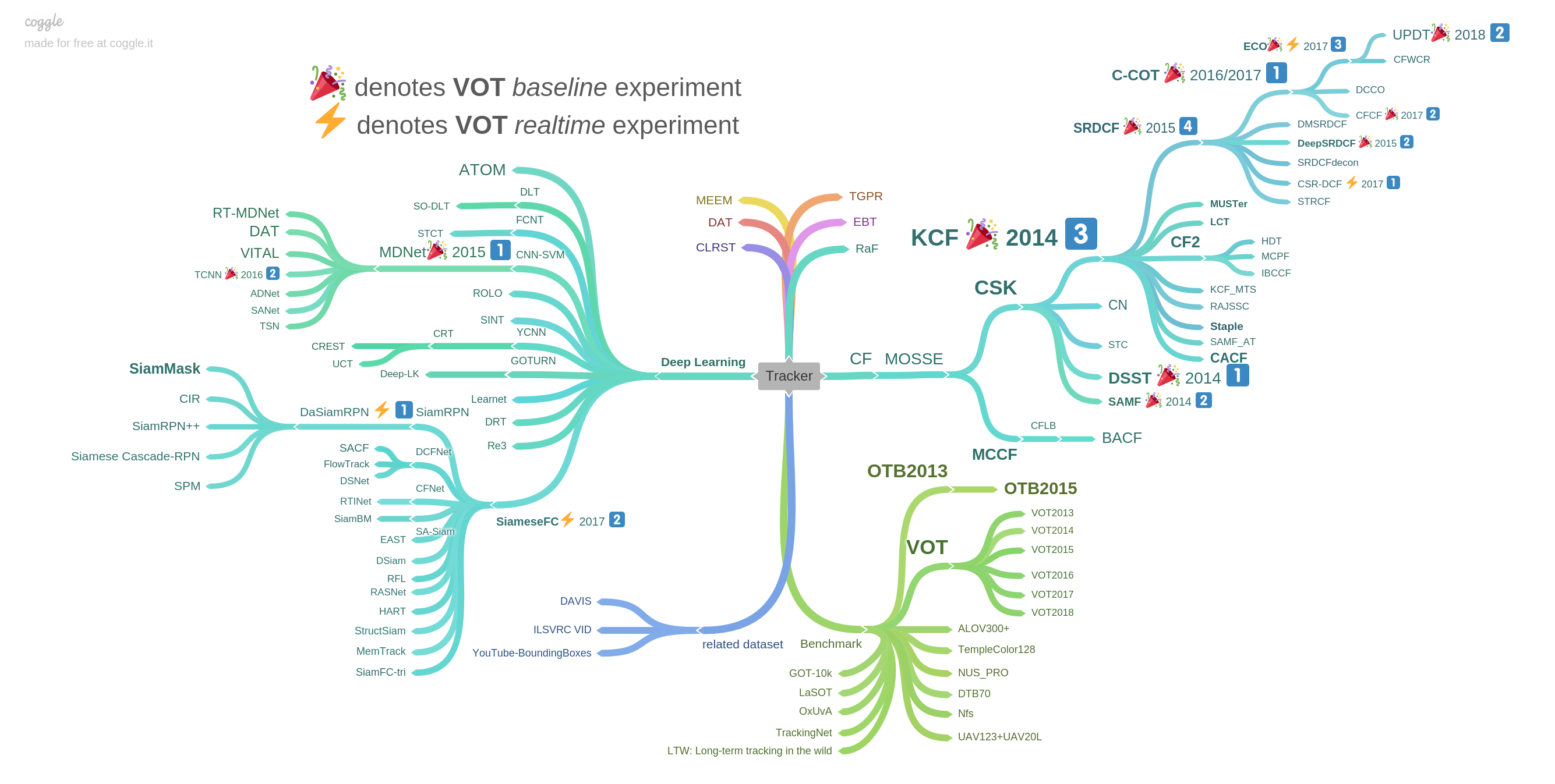
基于 深度学习 的方法在训练神经网络的时候会产生较多的参数,从而导致训练时间较长,难以达到实时追踪的目的。
基于 相关滤波 的方法速度快,并且追踪的效果好,逐步成为视频跟踪算法发展的主要方向。从图中可以看到,作为首次将 Correlation Filters 引入到 目标追踪 的 MOSSE 方法被称为该领域的 开山鼻祖 。
MOSSE 算法
该算法是在 2010 年由 《Visual object tracking using adaptive correlation filters》 论文提出的,其使用 MISSE(Minimum Output Sum of Squared Error filter,误差最小平方和滤波器) 来训练一个最优的滤波器模板,使其在目标上的响应最大,如下所示:
$$ g = f \star h \qquad(3) $$
其中,$ g $ 表示响应输出,即相关输出,$ f $ 表示输入图像,$ h $ 表示滤波模板,$ \star $ 为卷积操作。式 $ (3) $ 可以进一步展开,如下所示:
$$ (f \star h)(\tau) = \int_ {\infty} ^ {-\infty}{f ^ *}(t)h(t + {\tau})dt \qquad(4) $$
由于输入图像 $ f $ 是固定的,这里只需要确定的是滤波器模板 $ h $。由于上式的卷积运算计算量很大,因此 MOSSE 方法利用 快速傅里叶变换(FFT) 的方式,将 $ f $ 和 $ h $ 在频域内进行表示,函数互相关的傅里叶变换等于函数傅里叶变换的乘积(根据卷积定理可知:时域上的卷积等于频域上的乘积),将 卷积 操作转换为 点乘 操作,这样可以极大的减少计算量。也就是说,在这里将输入图像和滤波器通过算法变换到频域后,直接进行相乘,然后再变回时域(即图像的空域)就可以得到响应结果了。如下所示:
$$ \mathcal{F}(g) = \mathcal{F}(f \star h) = \mathcal{F}(f) \odot {\mathcal{F}(h) ^ *} \qquad(5) $$
$ \mathcal{F} $ 表示傅里叶变换,$ \odot $ 表示点乘运算(也就是点积运算)。可将 $ (5) $ 简写成如下所示:
$$ G = F \odot {H^*} \qquad(6) $$
也即:
$$ {H^*} = \frac {G}{F} \qquad(7) $$
好了,现在就只需要求 $ {H^*} $ 就可以了。
在计算之前,对于实际的目标追踪技术,还需要考虑到 目标的外观变换 等因素的影响。所以需要考虑到以目标的 $ m $ 个图像作为参考,从而提高滤波器模板的鲁棒性,如下所示:
$$ min_ {H^*}= \sum_ {i=1}^{m} {\mid} H^ * {\odot} F_{i} - G_{i} {\mid}^{2} \qquad(8) $$
其中,$ F_{i} $ 表示输入图像,$ G_{i} $ 表示在傅里叶域中期望的输出图像,目标是找到使输出误差平方和最小的滤波器 $ H^* $。
通常为了得到函数的最优值,可以通过对该函数求导数然后置为零即可。然而该函数表示的都是 实数值,即表示的是 复变量的实数值函数。
由于傅里叶域中的 相关 是逐个元素相乘的,所以这里可以独立地优化滤波器 $ H^ $ 中的每个元素。因此,优化问题可以从多元优化问题转换为独立地优化 $ H^ $ 中每个元素的问题。**
对于每个元素来说,要想找到最小的 $ min $,只需要将其中的每个元素的 MOSSE 都最小即可,如下所示:
$$ min_ {H_ {w,v}^*}= \sum_ {i=1}^{m} {\mid} H_ {w,v}^*F_{w,v,i} - G_{w,v,i} {\mid}^{2} \qquad(9) $$
$ w $ 和 $ v $ 是 $ H^* $ 中每个元素的索引。
要想得到最小的 $ {H_ {wv}^{*}} $,只需要将上式求偏导,并使偏导等于 $ 0 $ 即可,如下所示:
这里要注意的是,在 复数域 的求导和在 实数域 求导是不同的。
$$ 0 = \frac {\partial}{\partial H_ {w,v}^{*}} \sum_{i=1}^{m} {\mid} H_{w,v}^*F_{w,v,i} - G_{w,v,i} {\mid}^{2} \qquad(10) $$
$$ \Rightarrow 0 = \frac {\partial}{\partial H_ {w,v}^{*}} \sum_{i=1}^{m} (H_{w,v}^*F_{w,v,i}-G_{w,v,i})(H_{w,v}^*F_{w,v,i}-G_{w,v,i}) ^ * $$
$$ \Rightarrow 0 = \frac {\partial}{\partial H_ {w,v}^{*}} \sum_{i=1}^{m} (H_{w,v}^*F_{w,v,i}-G_{w,v,i})(H_{w,v}F_{w,v,i} ^ * - G_{w,v,i} ^ *) $$
$$ \Rightarrow 0 = \frac {\partial}{\partial H_ {w,v}^{*}} \sum_{i=1}^{m} (H_{w,v}^*F_{w,v,i} {\cdot} H_{w,v}F_{w,v,i} ^ *- H_{w,v}^*F_{w,v,i} {\cdot} G_{w,v,i} ^ * - H_{w,v}F_{w,v,i} ^ * {\cdot} G_{w,v,i} + G_{w,v,i} {\cdot} G_{w,v,i} ^ *) $$
$$ \Rightarrow 0 = \sum_{i=1}^{m} (F_{w,v,i} {\cdot} H_{w,v}F_{w,v,i} ^ * - F_{w,v,i} {\cdot} G_{w,v,i} ^ *) $$
$$ \Rightarrow \sum_{i=1}^{m} F_{w,v,i} {\cdot} H_{w,v}F_{w,v,i} ^ * = \sum_{i=1}^{m}F_{w,v,i} {\cdot} G_{w,v,i} ^ * $$
$$ \Rightarrow H_{w,v} = \frac {\sum_{i=1}^{m}F_{w,v,i} G_{w,v,i} ^ *}{\sum_{i=1}^{m} F_{w,v,i} F_{w,v,i} ^ *} \qquad(11) $$
其中,$ (11) $ 表示的是每个元素的值,按以上方式处理所有 $ H $ 中的元素,可以得到 滤波器模型的公式:
$$ H = \frac {\sum_{i=1}^{m}F_{i} {\odot} G_{i} ^ *}{\sum_{i=1}^{m} F_{i} {\odot} F_{i} ^ *} \qquad(12) $$
在原文中,作者对跟踪框(GroundTruth)进行随机变换,获取一系列的训练样本 $ f_ {i} $,而 $ g_ {i} $ 是由高斯函数产生的,其峰值的位置就是在 $ f_ {i} $ 的中心位置。获得了一系列的训练样本和结果之后,就可以计算滤波器模板 $ h $ 的值了。
然而,在目标跟踪过程中,只需要将 $ (12) $ 这一滤波器模板与当前帧的图像做 相关操作 即可,将得到的响应结果中最大的点所对应的坐标作为当前帧的位置(相当于在二维平面上移动模板)。考虑到想要让滤波器对形变、光照等外界因素的影响具有更好的鲁棒性,采取了以下模板更新策略:
$$ H_ {t} = \frac {A_ t}{B_ t} \qquad(13) $$
$$ A_ {t} = \eta F_ {t} \odot G_ {t} ^ * + (1 - \eta) {A_ {t-1}} \qquad(14) $$
$$ B_ {t} = \eta F_ {t} \odot F_ {t} ^ * + (1 - \eta) {B_ {t-1}} \qquad(15) $$
$ H_ {t} $ 表示在第 $ t $ 帧求得的滤波模板,$ \eta $ 为经验常数。这里将滤波器模板被拆分为 分子 和 分母 两部分,分别对这两部分进行更新。其中 $ A_ {t} $ 和 $ A_ {t-1} $ 分别表示当前帧和上一帧。
对于其他的部分,比如可以向 $ (12) $ 中引入正则化参数,或者分别求 $ H_ {i} $ 然后再取平均值等。
2D-FFT
来看一下,在 Matlab 中 二维傅里叶变换(fft2) 是怎么进行的。
$$ Y_{p+1,q+1} = \sum_{j=0}^{m-1} \sum_{k=0}^{n-1} {w_{m}^{jp} w_{n}^{kq} X_{j+1,k+1} } $$
其中, $ w_m $ 和 $ w_n $ 是复单位根,即:
$$ w_m = e^{\frac{-2πi}{m}} $$
$$ w_n = e^{\frac{-2πi}{n}} $$
$ i $ 是虚数单位,$ p $ 和 $ j $ 表示从 $ 0 $ 到 $ m-1 $ 范围的索引,$ q $ 和 $ k $ 表示从 $ 0 $ 到 $ n-1 $ 范围的索引,$ +1 $ 表示将 $ X $ 和 $ Y $ 的索引平移 1 位。