《剑指 Offer》中涉及到了约瑟夫环问题，虽然下面文章中所描述的和书中的题目有些差异，但从总体上看，都涉及到了约瑟夫环问题。

题目描述

0，1，···，n-1 这 n 个数字排成一个圆圈，从数字 0 开始，每次从这个圆圈里删除第 m 个数字。求出这个圆圈里剩下的最后一个数字。

而本文所涉及到的题目如下所示： 有很多人围成一个圈，由第 1 个人开始报数，报数到 3 的人就出队，然后再由下一个人重新从 1 开始报数，报数到 3 的那个人再出队，就这样直到剩下最后一个人。

你可以看到，这两个题目所描述的有些不同。第二题与第一题的不同之处在于：每次需要由下一个人重新从 1 开始报数，则最后剩下的那个人必然就是 1。

输入：一个环形单向链表的头节点 head 和报数的值 m。

输出：最后生存下来的节点，且这个节点自己组成环形单链表，其他节点都删除掉。

时间复杂度：O(N)

方法一

分析

首先根据题目的描述，走一遍这个流程。假如报数的值 m = 3，也就是需要删除的编号，如下图左侧所示。删除 3 后，则将原来的 4 置为 1， 5 置为 2， 1 置为 3， 2 置为 4，如下图右侧所示：

然后同样的再删除第三个数 3，则原来的 4 变成了 1，原来的 1 置为 2，原来的 2 置为 3，如下图所示：

然后再从 1 开始，删除第 3 个数，如下所示：

然后再从 1 开始数三个数，结果又回到了 1，即将这个 1 删除后，再将 2 变为 1，这就得到了最后的结果。如下图所示：

好，知道以上计算流程之后，我们再看看如何具体的分析这个问题。

我们 从后往前计算，每报一次数，然后链表中的下一个节点就重新编号，那么最后所剩节点的个数只有一个。并且可以确定的是，最后该节点一定是 1（如上图所示）。

那么现在需要找到一个公式，能够从底往上推出初始的状态，如下所示：

从 1 开始计算，一直计算到剩余节点数 N，此时对应的 存活节点的编号 就是在原链表中一个也没有报数的情况下所对应的节点，我们最后返回该节点即可。也就是说，我们一开始是不知道哪个节点最后是剩余的，而只知道最后那个剩余节点的编号一定是 1。

现在假设链表长度为 i，则每个节点的 编号 和 报数 之间的关系，如下所示：

我们可以将其绘制出来，如下所示：

然而，上面的图像是如何得到的呢？

这里可以对下面的图像进行平移，向右移动一位，再向上移动一位，从而得到上面的图像。

因此，可以得到 编号 和 报数 之间的关系：编号 = (报数 - 1) % i + 1。

如何平移？

左加右减，上加下减。

好，找到了 编号 和 报数 之间对应的关系之后，我们再看 新编号 和 老编号 之间的关系。当链表长度为 i 的时候，它们之间的关系如下所示：

S 表示被删除的节点。

新号是由于删除了节点 S，才变成长度为 i - 1 的。

由于 S 节点被删除了，所以它在新号中就没有编号了。原来在老编号中的 S+1，在新编号中就变成了 1。原来在老编号中的 S-1，在新编号中就变成了 i-1（因为新编号的长度就是 i-1）。

下面进行详细说明，如下图所示：

首先删除 3，然后从 4 的位置开始重新编号为 1。这里找一下对应的关系。新编号为 1 的时候，老编号为 4，也就是 S+1=3+1=4；新编号为 2 的时候，老编号为 5，也就是 S+2=3+2=5；…；新编号为 6 的时候，也就是 i-S=9-3=6，老编号为 9；新编号为 7 的时候，也就是 i-S+1=9-3+1=7，老编号回到了 1。

这里用如下坐标形式将上面的内容进行表示：

也就是说，新编号的 1 对应旧编号的 S+1，新编号的 i-S 对应旧编号的 i，新编号的 i-S+1 对应旧编号的 1，新编号的 i-1 对应旧编号的 S-1。此时 S 位置上的数已经被删除了。

现在将上图中的线延长，如下所示：

由于之前已经求出了函数：编号 = (报数 - 1) % i + 1，将该函数向左平移 S 个单位，就可以得到上图。过程如下：

从而可以得到对应关系：旧编号 = (新编号 - 1 + S) % i + 1。

由之前的对应关系可知：数到第 m 个就报数，当前报数的编号就是 S，则有：S = (m - 1) % i + 1。由于 m 已知，则将 S 带入到上式中，就可以求出 新编号 和 老编号 对应的关系。如下所示：

$$ 旧编号 = (新编号 - 1 + S) % i + 1 $$ $$ 旧编号 = [新编号 - 1 + (m - 1) % i + 1] % i + 1 $$ $$ 旧编号 = [新编号 + (m - 1) % i] % i + 1 $$ $$ 旧编号 = (新编号 + m - 1)% i + 1 $$

这里说一下最后两步为什么相等？

用 $ (a+k % i) %i $ 表示倒数第二个式子，用 $ (a+k) %i $ 表示倒数第一个式子。

假设 $ k=c \cdot i + t $，其中 $ t $ 表示余数，则有 $ (a+k % i) %i = (a+t) % i $。而 $ (a+k) %i = (a+t) % i $，所以 $ (a+k % i) %i = (a+k) %i $。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

public class Solution {
    public static class Node {
        int val;
        Node next;

        Node(int val) {
            this.val = val;
        }
    }

    // 用链表模拟环
    public static Node lastRemaining_Solution(Node head, int m) {
        if (head == null || head.next == head || m < 1) {
            return head;
        }

        Node cur = head.next;
        int temp = 1;
        while (cur != head) {
            temp++;
            cur = cur.next;
        }

        temp = getLive(temp, m);
        while (--temp != 0) {
            head = head.next;
        }
        head.next = head;
        return head;
    }

    // 核心代码
    private static int getLive(int i, int m) {
        if (i == 1) {
            return 1;
        }
        return (getLive(i - 1, m) + m -  1) % i + 1;
    }
}

对代码的详细解释：

https://github.com/dyfloveslife/LeetCodeAndSwordToOffer/blob/master/src/SwordToOfferSolution/_62_LastNumberInCircle/Solution.java

方法二

这是在力扣的解答区看到的方法，讲得比较清晰，因此在这里做一个梳理。

该方法的核心在于：只关心最终活着的那个人的序号变化情况，从最终结果反推出规律。

例如一共有 n=8 个人，每当数到 m=3 的时候就将该人给杀掉，我们用 F(n, m) 来表示最后剩下的那个人的序号。整个流程如下图所示：

图片均来自【参考】文章。

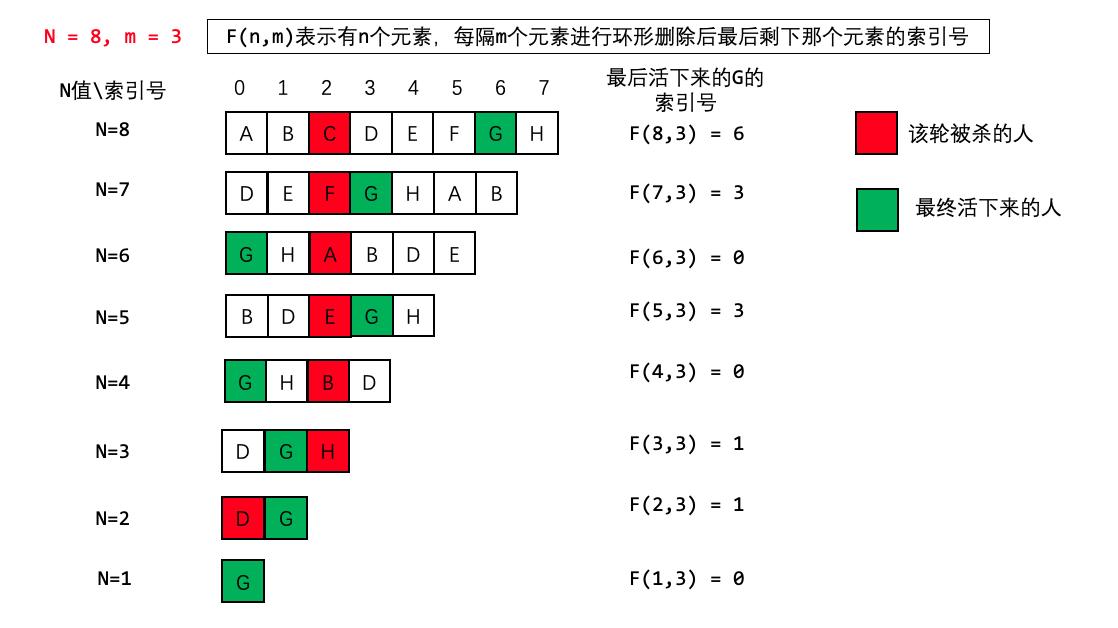
从上图可以看到，我们将这 8 个人用字母代替，在每一轮中，红色的方格表示当前需要被杀掉的人，绿色的方格表示最终存活下来的人。N=8 时，将 C 杀掉，则下一轮（N=7）将会从 D 开始报数，然后往右数 m=3 个数，再将 F 杀掉，以此类推。

此外，注意观察每一轮中最后活下来的 G 的索引变化情况。当最后只剩下一个人的时候，这个人的编号（索引号）一定是 0。

接下来我们看看如何进行反推，例如如何从 N=7 反推出 N=8 时的情况，如下图所示：

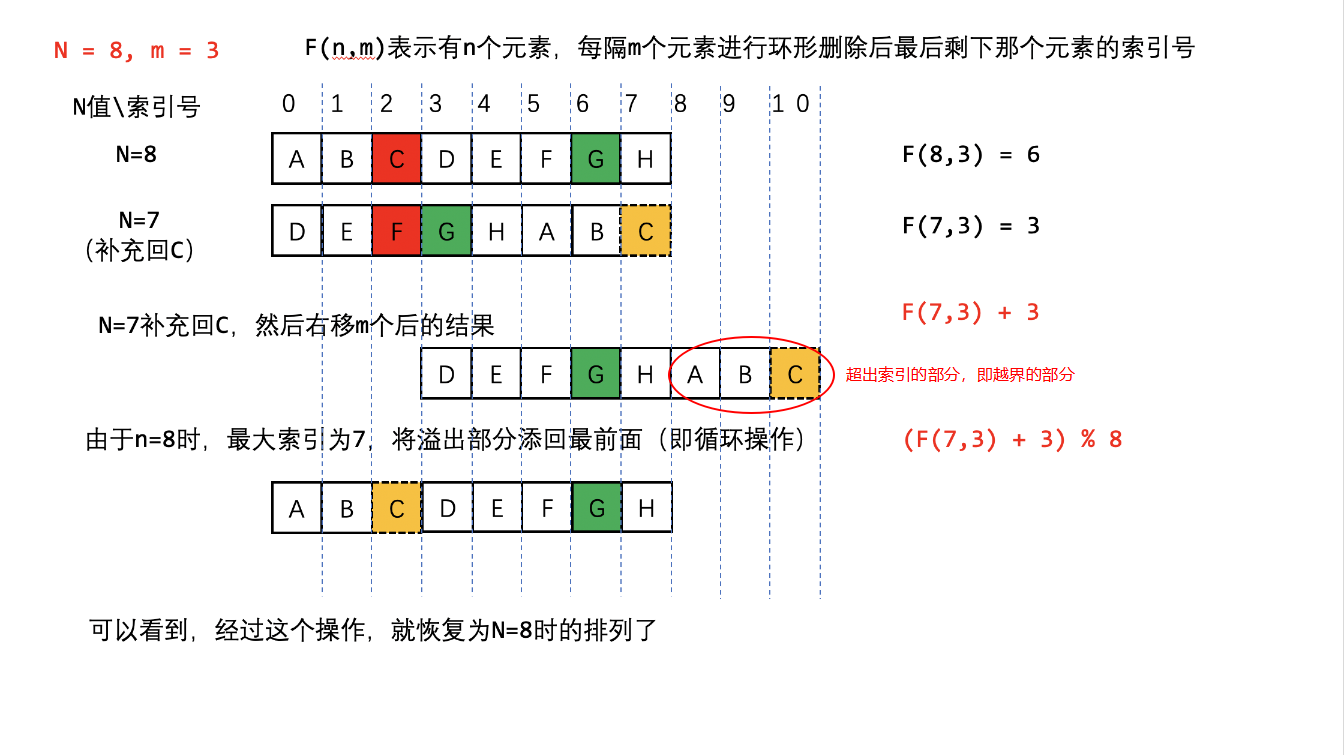
在从 N=7 回到 N=8 的过程中，先将被杀掉的 C 补充回去，即黄色方格；然后将 N=7 右移 m 个单位，由于多出 3 个人（A、B、C）越界了，因此将它们移到前面；最后得到的结果就和 N=8 一样了。

因此，从 N=7 到 N=8 的递推公式为：$f(8, 3)=[f(7, 3) + 3] % 8$，而将此公式推广到一般情况，则有：$f(N, m)=[f(N-1, 3) + 3] % N$。

最后整理得到的递推公式：

$$ 当 n=1 时，f(N, m) = 0 $$

$$ 当 n > 1 时，f(N, m) = [f(N-1, m) + m] % N $$

代码

1
2
3
4
5
6
7
8
9

public int lastRemaining(int n, int m) {
    // 最终活下来的那个人的初始位置
    int pos = 0;
    for (int i = 2; i <= n; i++) {
        pos = (pos + m) % i;
    }
    
    return pos;
}

参考

• https://leetcode-cn.com/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof/solution/huan-ge-jiao-du-ju-li-jie-jue-yue-se-fu-huan-by-as/