KMP 算法适用于求解字符串匹配的问题，网上有许多文章对它都有详细的解释，之前在学习数据结构的时候也对该算法有些了解，但一直没怎么总结。先将其进行回顾，并写下此文，以作备忘。

KMP 算法是要实现这么一个问题：给定一个原始的字符串str1 = bbcabcdababcdabcdabde，我想知道这里面是否包含一个子串str2 = abcdabd。如果存在，则返回子串中的第一个字符在原始字符串中的索引，否则返回-1。

一般的解决思路可以使用暴力方法，即从 str1 的 0 位置开始逐个和 str2 开始匹配，如果有一位不相等的话，则再从 str1 的 1 位置开始与 str2 开始匹配，以此类推，一直比较下去，直至结束。

假如 str1 的长度为 N，str2 的长度为 M，在 N >= M 的前提下，该方法的时间复杂度为 O(N * M)。其中 N 一定是大于等于 M 的，假设 N 小于 M 的话，则 str2 构不成 str1 的子串，则就不符合题意了。

这种解法显然不是我们要的答案，接下来在介绍一种更快的方法之前，还有一个知识点需要提前说一下，就是公共前缀与公共后缀的问题。

最长公共前缀和最长公共后缀

前缀：除了最后一个字符，其它字符所构成的字符串。

后缀：除了第一个字符，其它字符所构成的字符串。

例如，对于字符串abcabcd，求字符d的在此字符串中的前缀和后缀。我们先看前缀，字符d的前缀有a、ab、abc、abca、abcab，注意，abcabc虽然也是其前缀，但我们规定不能包括最后一个字符，所以不考虑abcabc。

再来看d的后缀，有c、bc、abc、cabc、bcabc，注意，abcabc虽然也是其后缀，但我们规定不能包括第一个字符，所以这里也不考虑abcabc。

而对于最长公共前缀和最长公共后缀来说，就是前缀和后缀中公共且最长的部分，即abc。如下图所示：

分析

之所以暴力算法的时间复杂度很高，是因为它重复比较了多次，为了加速字符串的比较过程，我们还需要用到一个next数组，该数组记录了字符串 str2 中每个字符的最长公共前缀和最长公共后缀的长度。现在先将其理解为一个黑盒，暂时不用管它是怎么实现的，后面会讲到。

假如 str1 的 i 位置与 str2 的 0 位置开始匹配，直到 X 和 Y 位置出现了不匹配的情况时，原来的方法是将 str2 的 0 位置再次来到 str1 的 i+1 位置再次开始匹配，然而现在不这么做。现在先根据next[]中 Y 的最长前缀和最长后缀的匹配长度，让 str2 的 0 位置来到 str1 的 j 位置，由于 str1 中从 j 位置开始的某些字符与 str2 中从 0 位置开始的字符是相同的，所以这里直接从 Z 位置与 X 位置开始匹配。如下图所示：

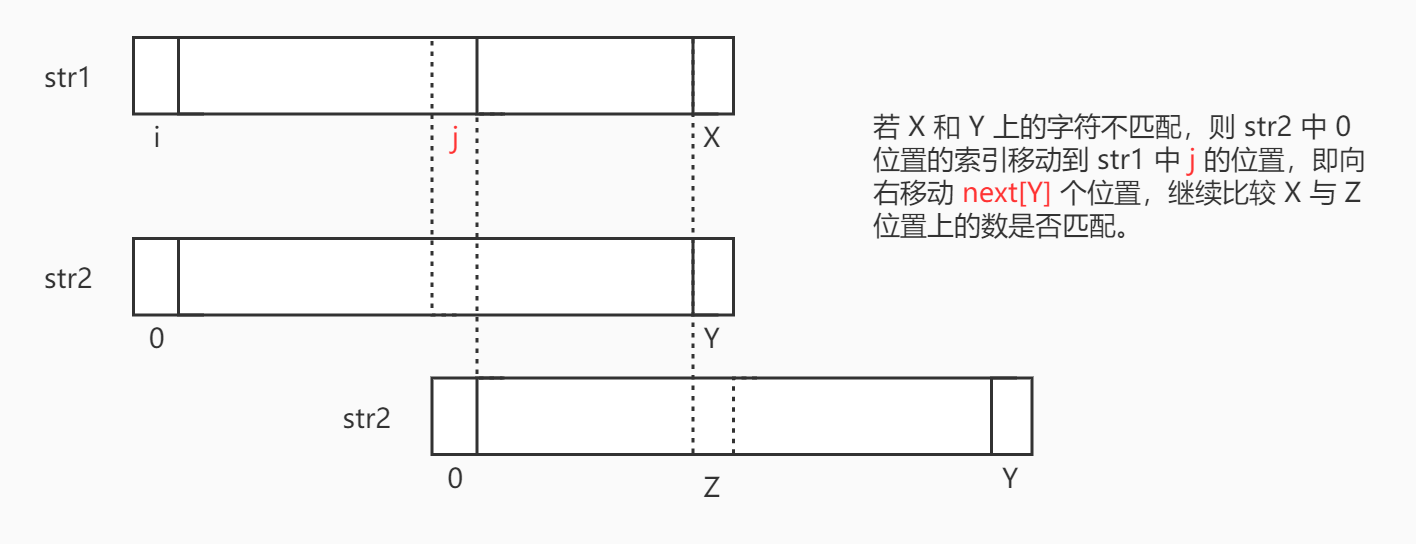
如下图所示，X 位置上的 t 与 Y 位置上的 a 不同，所以 str2 中的 0 位置来到了 str1 中的 j 位置，让 X 位置上的 t 和 Z 位置上的 a 进行比较。

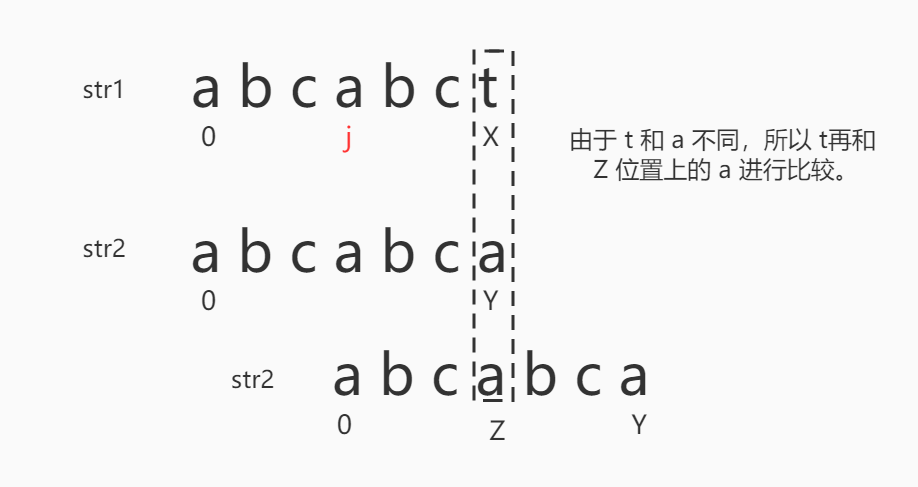
由于 Z 位置的 a 与 t 还是不同的，所以在查next[Z]的时候，此时 Z 已经没有公共前缀和后缀了，所以最后abcabca不是abcabct的子串。注意：如果 str1 中的 t 后面还有字符的话，则 str2 在没有匹配到的时候，str2 还需要与 X+1 位置上的字符开始比较。

next 数组

对于如何求 next 数组：

0 位置为 -1；
1 位置为 0；
对于 2 位置上的值，如果 nums[0] 和 nums[1] 相等，则为 1，否则为 0；
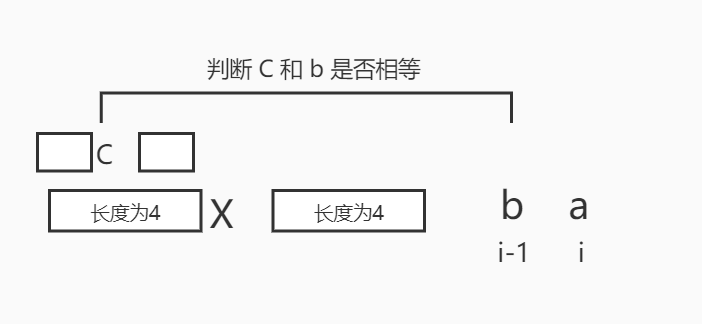
对于其它的位置，假如现在准备求 i 位置上的值，假设已知 i-1 位置上的值是 4，那么就看一下长度为 4 的下一个字符 X 等不等于 b，如果等于 b，则 i 位置的值为 5。

如果相等，则 i 的值为X在数组中的值+1，如下图所示：

如果不相等，则看 X 之前的最长前缀的下一个字符（这里假设是 C）是否和 b 相等，如果相等，则 a 的值就是 C 在 next 数组中的值+1，否则再继续往前找，直到找不到的时候，那 a 的值就是 0。如下图所示：