本文用于将常见的排序算法做一个总结。
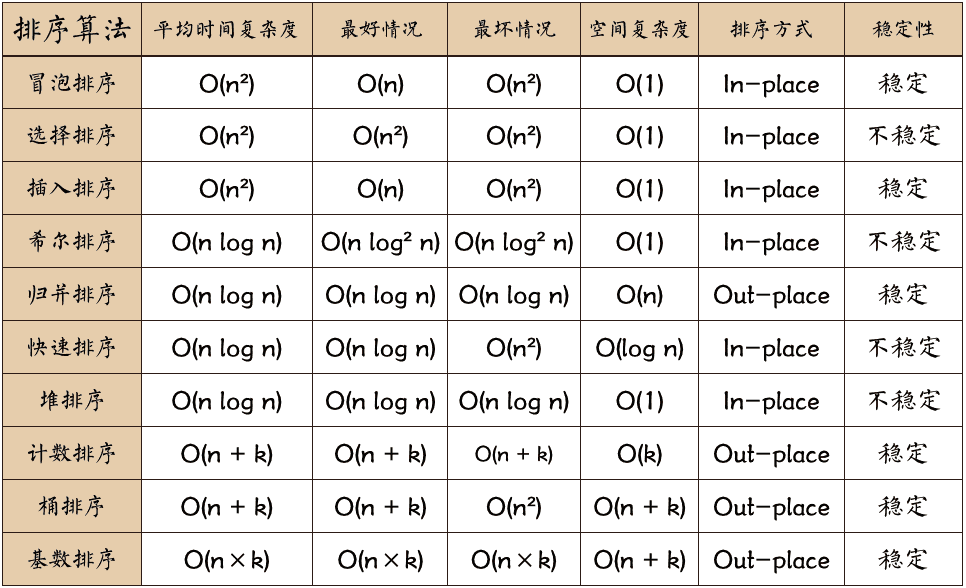
排序算法总览表
本文所涉及到的排序算法如下所示:
冒泡排序
冒泡排序是每两个元素之间进行比较的排序,如果规定排序后的数组满足从小到大的顺序的话,那么每一趟排序之后,都会将最大的那个元素放在右侧最终的位置上。也就是说,在每一趟排序之后,都会确定一个元素它的最终位置。通过外层循环控制每趟比较的元素个数,内层循环进行两两比较。如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
public int[] bubbleSort(int[] nums) {
if (nums == null || nums.length == 0) {
return new int[0];
}
for (int end = nums.length - 1; end >= 0; end--) {
for (int i = 0; i < end; i++) {
if (nums[i] > nums[i + 1]) {
swap(nums, i, i + 1);
}
}
}
return nums;
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
|
当然,还可以进行优化。例如 [5, 4, 1, 2, 3],在进行两趟冒泡排序后的数组为 [1, 2, 3, 4, 5]。此时已经是排好序的了,那么就可以直接返回了。因此,可以在每次比较之前设置一个 isSorted = true,如果存在比较了,则说明不是有序的,那么将其置为 false。在一趟比较完之后,如果 isSorted 还是 true,则说明数组已经是排好序的了,那么最后直接返回即可。如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
public int[] bubbleSort(int[] nums) {
if (nums == null || nums.length == 0) {
return new int[0];
}
// 外层循环用于控制每趟比较元素的数量
for (int end = nums.length - 1; end >= 0; end--) {
boolean isSorted = true;
// 内层循环用于两两比较
for (int i = 0; i < end; i++) {
if (nums[i] > nums[i + 1]) {
swap(nums, i, i + 1);
isSorted = false;
}
}
if (isSorted) {
break;
}
}
return nums;
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
|
假设有 $n$ 个元素的话,第一趟比较的元素是从 $0$ 到 $n-1$,共需要比较 $n$ 个数;第二趟比较的元素是从 $0$ 到 $n-2$,共需要比较 $n-1$ 个数,以此类推。
- 在最坏的情况下,有 $(n-1)+(n-2)+(n-3)+…+1=n(n-1)/2$,因此最坏时间复杂度为 $O(n^{2})$。
- 在最好的情况下,数组是有序的,只需要遍历一次数组就可以了,因此最好时间复杂度为 $O(n)$。
- 因此,平均时间复杂度为 $O(n^{2})$。需要注意的是,我们在计算平均时间复杂度的时候,是按照最坏时间复杂度进行计算的。
- 由于没有使用到额外的存储空间,因此空间复杂度为 $O(1)$。
- 由于相同两个数不会交换,因此冒泡排序是稳定的排序算法。
选择排序
选择排序的核心思想是:每次从后面未排序元素中选择一个最小的元素放在已排序元素后面,当然,所选出的这个元素肯定是比已排序元素大的。例如,从 $0$ 到 $n-1$ 选择一个最小的元素放在 $0$ 位置,接着从 $1$ 到 $n-1$ 中选择一个最小的元素放在 $1$ 位置,再从 $2$ 到 $n-1$ 中选择一个最小的元素放在 $2$ 位置,以此类推。这样的话,对于每一趟的选择,都会确定出该元素的最终位置。
其实,放在指定的位置这个操作相当于直接交换两个元素。在未排序数组中找最小元素的时候,可以每次定义一个 minIndex,然后在遍历未排序数组的同时不断更新这个 minIndex。如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
public int[] selectSort(int[] nums) {
if (nums == null || nums.length == 0) {
return new int[0];
}
for (int i = 0; i < nums.length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < nums.length; j++) {
// 在未排序的数组中找最小元素,同时不断更新 minIndex
minIndex = nums[j] < nums[minIndex] ? j : minIndex;
}
swap(nums, i, minIndex);
}
return nums;
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
|
其实从上面的swap()操作可以看出,在还没有完全确定最小元素之前,这些交换动作都是无意义的。因此,可以在swap()操作外面进行一个if (minIndex != i)的判断,只有当 minIndex 被更新的时候,才与 i 进行交换。
- 对于交换操作,最好的情况下就是数组完全有序的情况,此时无需进行任何交换。但也需要 $O(n^{2})$ 的时间复杂度。
- 最坏的情况下,也就相当于倒叙的情况,每次都需要交换。时间复杂度也是 $O(n^{2})$ 的。
- 因此,平均时间复杂度为 $O(n^{2})$。
- 由于没有使用额外的存储空间,因此空间复杂度为 $O(1)$。
- 在进行
swap(nums, i, minIndex);的时候,有可能产生算法的不稳定性。例如 [5, 8, 5, 2, 9],第一次选择后面的 2 与第一个 5 进行交换,则此时数组中的两个 5 的相对位置发生了变化,因此是不稳定的。
插入排序
插入排序的核心思是:每一步将一个待排序的元素插入到已经排好序的有序序列中去,直到插完所有元素为止。如何插呢?插入排序每次对第 $k$ 个元素进行排序,此前的 $k-1$ 个已经是从小到大排好序的。在插入的时候从后往前遍历已排好序的序列,找到第一个小于当前元素的位置i,那么当前元素的位置就应该放在i的后面。
类似于我们平时打扑克牌,向已经排好序的牌中插入一个新的牌,只不过需要从后往前比较而已。其实这里的插入操作也是通过元素交换进行实现的。如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
public int[] insertionSort(int[] nums) {
if (nums == null || nums.length == 0) {
return new int[0];
}
// i=1 表示从索引 1 开始摸牌,也就是从 1 开始往后都是未排序的元素,
// 因此这里默认第一个元素(索引为 0)是已经排好序的
for (int i = 1; i < nums.length; i++) {
// j 先来到已排序序列的末尾元素,如果前面的数比后面的数大的话,则需要交换
for (int j = i - 1; j >= 0 && nums[j] > nums[j + 1]; j--) {
swap(nums, j, j + 1);
}
}
return nums;
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
|
事实上,将一个元素插入到一个有序数组中这个操作,可以不使用逐步交换。我们可以先赋值给一个临时变量,然后适当的元素后移,空出一个位置,最后把临时变量赋值给这个空位即可。如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
public int[] insertionSort(int[] nums) {
if (nums == null || nums.length == 0) {
return new int[0];
}
for (int i = 1; i < nums.length; i++) {
// 右手摸到一个牌,准备将它插入到已排序数组中
int get = nums[i];
// j 的位置是已排序数组的最后一个位置,也就是左手中最大的那张牌
int j = i - 1;
// 将抓到的牌与手牌进行从右往左的比较
while (j >= 0 && nums[j] > get) {
// 如果手牌比抓到的牌大,则将手牌往右移
// 也就是将手牌 j 放到 j+1 的位置
nums[j + 1] = nums[j];
j--;
}
// 直到该手牌比抓到的牌小(或相等),那么就将抓到的牌放在这个手牌的右边,
// 相等元素的相对次序不变,因此是稳定的
nums[j + 1] = get;
}
return nums;
}
|
可以看到,用摸牌这种游戏来想象插入排序的插入过程,这是非常有意思的,也很符合我们玩牌的操作。
- 最好的情况下,数组是有序的,那么只需要扫描一遍数组即可,因此时间复杂度是 $O(n)$。
- 最坏的情况下,数组是逆序的,那么对于每一个数来说,都需要一路换到底,因此时间复杂度是 $O(n^{2})$。
- 因此,平均时间复杂度是 $O(n^{2})$。
- 由于没有使用额外的存储空间,因此空间复杂度为 $O(1)$。
- 由于未排序的元素在向前扫描的过程中,遇到相同的元素就不会继续扫描了,更不会插在它的前面,因此插入排序是稳定的。
插入排序适用于短数组,因为短数组的特点是每个元素离它最终排定的位置都不会太远。因此,在小区间内执行排序任务的时候,可以使用插入排序。
归并排序
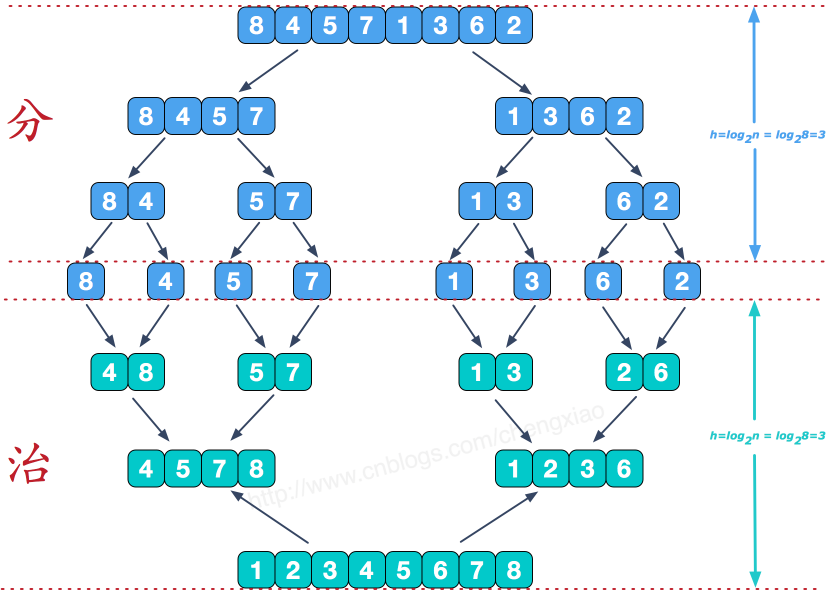
归并排序的核心思想是:将已经有序的子序列合并,得到完全有序的序列。也就是先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。其采用的是分治思想。
排序过程类似于一棵二叉树,如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
public int[] sortArray(int[] nums) {
if (nums == null || nums.length == 0) {
return new int[0];
}
mergeSort(nums, 0, nums.length - 1);
return nums;
}
private void mergeSort(int[] nums, int left, int right) {
if (left == right) {
return;
}
// 下面的注释表示:当 left 和 right 是大整数的时候,即使溢出,结果也是正确的
// int middle = (left + right) >>> 1;
int middle = left + ((right - left) >> 1);
mergeSort(nums, left, middle);
mergeSort(nums, middle + 1, right);
merge(nums, left, middle, right);
}
private void merge(int[] nums, int left, int middle, int right) {
int[] help = new int[right - left + 1];
int p1 = left;
int p2 = middle + 1;
int index = 0;
while (p1 <= middle && p2 <= right) {
// <= 是为了让相同的元素在原来靠前的位置,在排序后依然靠前,
// 因此,如果将 <= 改成 < 则丢失了稳定性
help[index++] = nums[p1] <= nums[p2] ? nums[p1++] : nums[p2++];
}
while (p1 <= middle) {
help[index++] = nums[p1++];
}
while (p2 <= right) {
help[index++] = nums[p2++];
}
for (int i = 0; i < help.length; i++) {
nums[left + i] = help[i];
}
}
|
- 最好和最坏的情况下,时间复杂度都是 $O(nlogn)$。
- 这是因为每次合并的操作是 $O(n)$,而树的深度是 $logn$,因此平均时间复杂度也是 $O(nlogn)$。
- 由于需要使用额外的数组空间,因此空间复杂度是 $O(n)$。
- 归并排序是稳定的,具体原因已在注释中给出。
快速排序
快速排序的核心思想是:每一次的排序之后都确定一个元素处于最终的位置,然后递归地对左部分和右部分进行排序,直到数组有序。其利用了分治思想,与归并排序不同的是,快速排序在分的时候不会一分为二,而是采用了 partition 的方法来选择一个枢纽。因此,这个枢纽选择的好坏将影响快速排序的速度。
在进行 partition 选择枢纽的时候,要采用随机的方式进行选择,否则如果输入的序列是有序或逆序数组的话,快速排序会非常慢。这里有三种不同的版本:
- 基本快排:将元素都划分到了枢纽的一侧,可能会造成递归树的倾斜;
- 双指针快排:将元素等概率的划分到了枢纽的两侧,递归树相对平衡。也就是将数组中小于枢纽的元素放在枢纽的左边,大于枢纽的元素放在枢纽的右边;
- 三指针快排:将数组中小于枢纽的元素放在枢纽的左边,大于枢纽的元素放在枢纽的右边,等于枢纽的元素放在中间。
如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
|
public int[] quickSort(int[] nums) {
if (nums == null || nums.length < 2) {
return new int[0];
}
quickSortCore(nums, 0, nums.length - 1);
return nums;
}
private void quickSortCore(int[] nums, int left, int right) {
if (left < right) {
// 随机快排
Random random = new Random();
// 从数组中随机选择一个索引,将该索引上的数与数组中最后一个数进行交换
// int randomIndex = (int) (left + Math.random() * (right - left + 1));
int randomIndex = left + random.nextInt(right - left + 1);
swap(nums, randomIndex, right);
int[] p = partition(nums, left, right);
quickSortCore(nums, left, p[0] - 1);
quickSortCore(nums, p[1] + 1, right);
}
}
// 荷兰国旗问题(稍微有些不同)
// 该函数返回的是等于数组最后一个元素 x 范围内的左右边界
// p[0] 代表等于 x 的左边界,p[1] 代表等于 x 的右边界
private int[] partition(int[] nums, int left, int right) {
int less = left - 1;
// 这里将大于 x 的区域的范围直接定位到 right
int more = right;
while (left < more) {
// 小于 num 的情况
if (nums[left] < nums[right]) {
swap(nums, ++less, left++);
// 大于 num 的情况,此时 left 需要留在原地,继续考察与 num 的大小关系
} else if (nums[left] > nums[right]) {
swap(nums, --more, left);
// 等于 num 的情况
} else {
left++;
}
}
// 由于改进后的 partition 函数,初始的时候大于 x 的区域是包含 x 的,所以在划分完之后,
// 需要将最后一个 x 的位置与 大于 x 区域的第一个数交换,这样就实现了小于 x 的在左边,
// 等于 x 的在中间,大于 x 的在右边
// 也就是说 x 一开始就不参与遍历,最后通过 swap 让其归位
swap(nums, more, right);
return new int[]{less + 1, more};
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
|
- 快速排序与输入的数据规模有关,最坏的情况下,如果输入的序列是有序的,例如 [1, 2, 3, 4, 5],如果每次都选择最后一个数进行划分,那么对于每一个数都需要 $O(n)$ 的时间,因此时间复杂度就是 $O(n^{2})$。
- 最好的情况下,如果划分的好,划分得均匀,左右部分的数据规模大体相同的话,时间复杂度就是 $O(nlogn)$。
- 对于随机快排,也就是每次从数组中随机选择一个数之后,与数组中最后一个数进行交换,用这个随机选择的数进行划分。这就变成了一个概率问题,因此长期期望是 $O(nlogn)$。
- 由于在递归过程中使用到了递归函数的栈空间,因此空间复杂度取决于递归树的深度,即 $O(logn)$。
- 快速排序是不稳定的,不稳定性发生在枢纽元素与最后一个元素交换的时刻。例如 [1, 3, 4, 2, 8, 9, 8, 7, 5],枢纽元素是 5,在一次划分后 5 需要和第一个 8 进行交换,从而改变了两个 8 的相对次序。
- 这里多说一句,Java 中的 Arrays.sort() 函数,它对于基础类型,底层使用的是快速排序,而对于非基础类型,底层使用的是归并排序。
- 这是因为对于基础类型,相同的值是无差别的,排序前后相同值的相对位置并不重要,因此使用了不稳定的快速排序;
- 而对于非基础类型,排序前后相同实例的相对位置不宜改变,因此选择稳定的归并排序。
堆排序
很多情况下会有这种需求:在收集一些元素的同时,处理当前最大的元素,然后再收集更多的元素,再处理当前最大的元素,如此循环。而优先队列就可以实现这种功能,它可以实现删除最大元素操作以及插入元素操作。
二叉堆类似于一个完全二叉树,通过某个节点可以找到它的父节点以及孩子节点。例如,如果位置 $k$ 的节点的父节点为对 $k/2$ 进行下取整,而位置 $k$ 节点的的左右孩子分别为 $2k$、$2k+1$。因此,得到它们之间的关系之后,就可以将它们放在数组中,使用数组来实现堆结构。
对于一个大根堆来说,需要满足子节点的值总是小于它的父节点的值这一定义。在建立大根堆的时候,需要实现一个不断向堆中放入元素的过程中,称之为 heapInsert。该元素插入到堆中之后,如果不满足堆的定义,则需要进行堆化处理,称之为 heapify,也就是将原本不满足堆定义的结构调整成堆结构。
但是,当我们具体实现的时候,当前节点与父节点和孩子节点之间的关系可能会有所不同。虽说是不同,但实现方式是一样的。如下所示:
1
2
3
4
5
6
7
8
9
10
|
+---+---+---+---+---+---+---+
| | | | | | | |
+---+---+---+---+---+---+---+
0 1 2 3 4 5 6
0
/ \
1 2
/ \ / \
3 4 5 6
|
将二叉树中的每个节点放到数组中,满足节点 $i$ 的左孩子为 $2i+1$,右孩子为 $2i+2$,父节点为 $(i-1)/2$。需要注意的是,下面的这棵二叉树是我们想象出来的结构,而真正使用到的是上面的数组。也就是说,当我们实现堆排序时,归根到底还是使用数组来模拟堆排序的过程。
给定一个乱序数组,如果将其建立成大根堆(或小根堆)?
建立大根堆的过程就是不断交换节点的过程,当某个元素放入到堆中以后,如果该节点比它的父节点大,则此时不满足大根堆的定义,因此需要将该节点与父节点进行交换。如果交换之后还不满足大根堆的定义,那么就一直向上交换,直到满足定义为止(相等的时候则不进行交换)。而找父节点的过程就是通过上面提到的通过索引进行实现的,实际的交换节点操作就是在数组中通过交换元素实现的。
建堆过程
假如 $0$ 到 $i-1$ 位置是已经建立好的大根堆,现在需要将 $i$ 位置上的数放进大根堆中,其实现逻辑如下所示:
1
2
3
4
5
6
7
8
9
|
public void heapInsert(int[] nums, int i) {
// 如果新插入进来的元素 nums[i] 比它的父节点大,
// 则进行交换,然后当前元素的索引就来到了父节点的索引位置。(也就是说,当前节点要向上跑)
// 直到当前节点小于它的父节点,while 循环才停止
while (nums[i] > nums[(i - 1) / 2] ) {
swap(nums, i, (i - 1) / 2);
i = (i - 1) / 2;
}
}
|
如果 $i$ 来到了 $nums[0]$ 位置,那么它的父节点就是 $nums[0 -1]/2=nums[0]$ 位置,因此 while 循环也会停止。以上通过将数组建立成一个大根堆的时间复杂度是 $O(n)$ 的。怎么分析?
如果向一棵二叉堆(完全二叉树)中插入一个元素,那么该元素只需要与它沿途的节点进行比较即可,也就是与树的高度有关。当第 $i$ 个节点加入到完全二叉树中的时候,它的时间复杂度是 $O(log(i - 1))$ 的。以此类推,当第 $i-1$ 个节点加入到完全二叉树中的时候,它的时间复杂度是 $O(log(i))$ 的。因此,可以得到 $log(1)+log(2)+log(3)+…+log(n-1)$,即时间复杂度为 $O(n)$。
调整过程
假如已经给定了一个大根堆,此时每个节点都是满足大根堆的定义的,即每个节点都大于它的所有的孩子节点。如果此时有一个节点的值变小了,那么就不满足大根堆的定义了,因此,我们需要一个重新调整的过程,让这个堆重新调整成大根堆,该过程称之为heapify。
如果某个节点的值变小了,那么如何进行调整,使之成为大根堆呢?
如果节点 A 变小了,那么需要找到它的左右孩子节点,先从左右孩子节点中选出最大的,然后将这个最大值与节点 A 进行比较:
- 如果这个最大值大于节点 A,则将它们进行交换(对应到数组中就是将元素进行交换),也就是让节点 A 往下沉;
- 如果这个最大值小于节点 A,则不进行交换。
过程如下所示,以下函数表示的是:从 $0$ 到 $heapSize$ 已经建立好了大根堆,但是 $i$ 上的元素变小了,因此我需要进行一系列调整的过程,也就是让 $i$ 往下沉的过程。
其中headSize表示堆中节点的数量,这个数量有可能小于等于数组中元素的个数,但肯定不会大于数组中元素的个数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
public void heapify(int[] nums, int i, int heapSize) {
// 拿到 i 的左孩子
int left = i * 2 + 1;
// 保证 left 不越界
while (left < heapSize) {
// 右孩子不越界,并且右孩子的值比左孩子的值大
int largest = left + 1 < heapSize && nums[left] < nums[left + 1] ? left + 1 : left;
// 上面的过程已经找到了左右两个孩子中较大的那个,
// 接下来需要和索引为 i 的进行比较
largest = nums[i] > nums[largest] ? i : largest;
// 如果在比较之后发现,最大值其实还是我自己,
// 说明 i 就不用往下沉了
if (largest == i) {
break;
}
swap(nums, largest, i);
// i 就变成了较大的那个孩子的下标
i = largest;
// 然后再拿到 i 的左孩子,进行下一次 while
left = i * 2 + 1;
}
}
|
以上就是建立堆以及调整堆的过程,那么如何进行堆排序呢?
每次将堆顶的元素与堆中的最后一个元素进行交换,一直到等个堆的大小减到 0 为止。如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
public void heapSort(int[] nums) {
if (nums == null || nums.length == 0) {
return;
}
for (int i = 0; i < nums.length; i++) {
heapInsert(nums, i);
}
// 当大根堆建立好以后,堆的大小就来等于数组的长度
int heapSize = nums.length;
// 将堆顶和堆中的最后一个元素进行交换
swap(nums, 0, --heapSize);
while (headSize > 0) {
// 由于堆中的最后一个元素被换到了堆顶,有可能不满足大根堆的定义,
// 因此需要堆化处理
heapfiy(nums, 0, heapSize);
// 在继续交换节点
swap(nums, 0, --heapSize);
}
}
|
- 堆排序是不稳定的,不稳定性发生在堆顶和其它节点交换的过程;
- 平均时间复杂度为 $O(nlogn)$;
- 由于只使用到了几个辅助变量,因此空间复杂度为 $O(1)$;
堆排序整体代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
public int[] sortArray(int[] nums) {
if (nums == null || nums.length == 0) {
return new int[0];
}
for (int i = 0; i < nums.length; i++) {
heapInsert(nums, i);
}
int heapSize = nums.length;
swap(nums, 0, --heapSize);
while (heapSize > 0) {
heapify(nums, 0, heapSize);
swap(nums, 0, --heapSize);
}
return nums;
}
private void heapInsert(int[] nums, int i) {
while (nums[i] > nums[(i - 1) / 2]) {
swap(nums, i, (i - 1) / 2);
i = (i - 1) / 2;
}
}
private void heapify(int[] nums, int i, int heapSize) {
int left = i * 2 + 1;
while (left < heapSize) {
int largest = left + 1 < heapSize && nums[left + 1] > nums[left] ? left + 1 : left;
largest = nums[i] > nums[largest] ? i : largest;
if (i == largest) {
break;
}
swap(nums, largest, i);
i = largest;
left = 2 * i + 1;
}
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
|
希尔排序
希尔排序的核心思想是:通过增量来将数组中的元素元素划分为不同的组,每个组内先进行排序,随着排序的进行,组会慢慢减少,而组内的元素会越来越多,数组整体也会越来越有序。
希尔排序是改进版的插入排序,与插入排序不同的是,它会优先比较距离较远的元素。如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
public int[] shellSort(int[] nums) {
if (nums == null || nums.length == 0) {
return new int[0];
}
int h = 1;
// 找增量的最大值
while (3 * h + 1 < nums.length) {
h = 3 * h + 1;
}
while (h >= 1) {
for (int i = h; i < nums.length; i++) {
// 插入排序
insertionSort(nums, h, i);
}
h = h / 3;
}
return nums;
}
// 这里的排序方法和插入排序相同
private void insertionSort(int[] nums, int h, int i) {
int get = nums[i];
int j = i - 1;
while (j >=0 && nums[j] > get) {
nums[j + 1] = nums[j];
j--;
}
nums[j + 1] = get;
}
|
- 由于只使用到了几个辅助变量,因此空间复杂度为 $O(1)$;
- 在时间复杂度方面,根据步长选择的不同而不同。最差的情况是 $O(n^{2})$,最好的情况是 $O(n)$;
- 此外,希尔排序也不是稳定的,因为这种元素间远距离的交换一般很难保证相同元素的相对位置。
以上都是基于比较的排序算法,而下面将要介绍到的都不是基于比较的排序算法,它们在排序的时候与被排序的样本的实际数据状况有关,所以在实际中不经常使用。
计数排序
计数排序的核心思想是:统计待排序数组中每个元素出现的次数,然后根据计数的大小,从小到大输出得到有序数组。由于用来计数的 Count 数组的长度取决于待排序数组中数据的范围,这使得计数排序对数据范围很大的数组,需要大量时间和内存,适用性不高。因此,计数排序适合对给定的范围内的数据元素进行排序。
例如,给定乱序数组 [2, 3, 2, 5, 3, 1],统计结果如下:
1
2
3
4
|
乱序数组: [2, 3, 2, 5, 3, 1]
出现的次数: 1 2 2 0 1
数字: 1 2 3 4 5
|
数字 1 出现了 1 次,数字 2 出现了 2 次,数字 3 出现了 2 次……因此在进行计数排序时,需要事先创建一个额外数组,额外数组的索引代表给定的待排序数组中元素的值,额外数组的值代表当前索引所出现的次数。如上图所示,将数字作为索引,将出现的次数作为额外数组的值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
public int[] countingSort(int[] nums, int k) {
if (nums == null || nums.length == 0) {
return new int[0];
}
int[] count = new int[k + 1];
for (int i = 0; i < nums.length; i++) {
count[nums[i]]++;
}
int index = 0;
for (int i = 0; i<= k; i++) {
while (count[i]-- > 0) {
nums[index++] = i;
}
}
return nums;
}
|
这里给定的 $k$ 表示基数,若果 $k=100$,则表示对 [0, 99] 内的整数进行排序。
- 计数排序是稳定的排序算法,因为是非比较的排序,因此元素之间的顺序不依赖元素之间的比较。
- 当输入的元素是 $n$ 个从 $0$ 到 $k$ 之间的整数时,它的时间复杂度是 $O(n+k)$,空间复杂度也是 $O(n+k)$。
基数排序
基数排序的核心思想是:对待排序数组中的元素先根据个位进行排序,然后再根据十位进行排序,然后再根据百位进行排序,直至排序完成。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
|
private static final int OFFSET = 50000;
public int[] radixSort(int[] nums) {
int len = nums.length;
// 预处理,让所有的数都大于等于 0,这样才可以使用基数排序
for (int i = 0; i < len; i++) {
nums[i] += OFFSET;
}
// 第 1 步:找出最大的数字
int max = nums[0];
for (int num : nums) {
if (num > max) {
max = num;
}
}
// 第 2 步:计算出最大的数字有几位,这个数值决定了我们要将整个数组看几遍
int maxLen = getMaxLen(max);
// 计数排序需要使用的计数数组和临时数组
int[] count = new int[10];
int[] temp = new int[len];
// 表征关键字的量:除数
// 1 表示按照个位关键字排序
// 10 表示按照十位关键字排序
// 100 表示按照百位关键字排序
// 1000 表示按照千位关键字排序
int divisor = 1;
for (int i = 0; i < maxLen; i++) {
countingSort(nums, temp, divisor, len, count);
int[] t = nums;
nums = temp;
temp = t;
divisor *= 10;
}
int[] res = new int[len];
for (int i = 0; i < len; i++) {
res[i] = nums[i] - OFFSET;
}
return res;
}
private void countingSort(int[] nums, int[] res, int divisor, int len, int[] count) {
// 1、计算计数数组
for (int i = 0; i < len; i++) {
// 计算数位上的数是几,先取个位,再十位、百位
int remainder = (nums[i] / divisor) % 10;
count[remainder]++;
}
// 2、变成前缀和数组
for (int i = 1; i < 10; i++) {
count[i] += count[i - 1];
}
// 3、从后向前赋值
for (int i = len - 1; i >= 0; i--) {
int remainder = (nums[i] / divisor) % 10;
int index = count[remainder] - 1;
res[index] = nums[i];
count[remainder]--;
}
// 4、count 数组需要设置为 0 ,以免干扰下一次排序使用
for (int i = 0; i < 10; i++) {
count[i] = 0;
}
}
private int getMaxLen(int num) {
int maxLen = 0;
while (num > 0) {
num /= 10;
maxLen++;
}
return maxLen;
}
|
- 基数排序是稳定的排序算法;
- 每一个关键字的桶分配都需要经过 $O(n)$ 的时间复杂度,而且分配之后得到的新的关键字序列又需要 $O(n)$ 的时间复杂度。假如待排序数据可分为 $d$ 个关键字,那么基数排序的时间复杂度为 $O(d * n)$;
- 而空间复杂度为 $O(n+k)$,其中 $k$ 表示桶的数量。
桶排序
桶排序的核心思想是:将待排序数组中的元素通过某种函数映射关系,映射到指定的桶中,对每个桶分别进行排序,然后将这些元素依次从桶中取出,形成最终有序的数组。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
// 桶排序
// 数据范围:
// 1 <= A.length <= 10000
// -50000 <= A[i] <= 50000
private static final int OFFSET = 50000;
public int[] bucketSort(int[] nums) {
int len = nums.length;
// 第 1 步:将数据转换为 [0, 10_0000] 区间里的数
for (int i = 0; i < len; i++) {
nums[i] += OFFSET;
}
// 第 2 步:观察数据,设置桶的个数
// 步长:步长如果设置成 10 会超出内存限制
int step = 1000;
// 桶的个数
int bucketLen = 10_0000 / step;
int[][] temp = new int[bucketLen + 1][len];
int[] next = new int[bucketLen + 1];
// 第 3 步:分桶
for (int num : nums) {
int bucketIndex = num / step;
temp[bucketIndex][next[bucketIndex]] = num;
next[bucketIndex]++;
}
// 第 4 步:对于每个桶执行插入排序
for (int i = 0; i < bucketLen + 1; i++) {
insertionSort(temp[i], next[i] - 1);
}
// 第 5 步:从桶里依次取出来
int[] res = new int[len];
int index = 0;
for (int i = 0; i < bucketLen + 1; i++) {
int curLen = next[i];
for (int j = 0; j < curLen; j++) {
res[index] = temp[i][j] - OFFSET;
index++;
}
}
return res;
}
private void insertionSort(int[] arr, int endIndex) {
for (int i = 1; i <= endIndex; i++) {
int temp = arr[i];
int j = i;
while (j > 0 && arr[j - 1] > temp) {
arr[j] = arr[j - 1];
j--;
}
arr[j] = temp;
}
}
|
- 桶排序也是稳定的排序算法;
- 最好的情况下,时间复杂度为 $O(n)$;
- 最坏的情况下,时间复杂度为 $O(n + k)$;
- 其实,桶排序的时间复杂度取决于各个桶之间数据进行排序的时间复杂度。如果桶划分得越小,各个桶之间的数据越少,那么所用的时间也会越少。但相应的空间复杂度就会增大。
- 空间复杂度为 $O(n+k)$。

